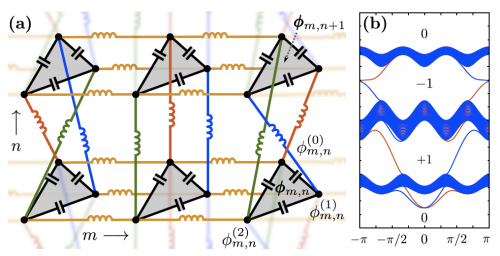
Our paper titled “Topological Properties of Linear Circuit Lattices” is published in PRL as editor’s suggestion.
Motivated by the topologically insulating circuit of capacitors and inductors proposed and tested by Jia et al. [arXiv:1309.0878], we present a related circuit with fewer elements per site. The normal mode frequency matrix of our circuit is unitarily equivalent to the hopping matrix of a quantum spin Hall
insulator, and we identify perturbations that do not backscatter the circuit’s edge modes. The idea behind these models is generalized, providing a platform to simulate tunable and locally accessible lattices with arbitrary complex spin-dependent hopping of any range. A simulation of a non-Abelian Aharonov-Bohm effect using such linear circuit designs is discussed.